Đề Thi Tuyển Sinh Lớp 6 – Toán & Tư Duy Logic
Trường THCS & THPT Trần Đại Nghĩa
Khóa ngày 04/07/2024
Bài 1. (6 điểm)
Có 100 chiếc lồng đèn được đánh số từ 1 đến 100. Bật sáng tất cả các lồng đèn, sau đó tắt các lồng đèn có số chia hết cho 3.
a) Hỏi có bao nhiêu lồng đèn đã tắt?
b) Tiếp tục tắt các lồng đèn có số chia hết cho 5. Hỏi sau hai lần tắt, có bao nhiêu lồng đèn còn sáng?
Điền kết quả vào ô trống:
a) _________ b) _________
Hướng dẫn chi tiết
Bài 1a
Đếm số lồng đèn có số chia hết cho 3 từ 1 đến 100:
- Các số chia hết cho 3 là: 3, 6, 9, 12, 15, 18, ..., 99
- Số lượng = lồng đèn đã tắt
Bài 1b
Số lồng đèn tắt sau hai lần:
- Đã tắt 33 lồng đèn có số chia hết cho 3
- Tiếp tục tắt các lồng đèn có số chia hết cho 5
- Từ 1-100 có số chia hết cho 5
- Nhưng trong đó đã có những số vừa chia hết cho 3 vừa chia hết cho 5 (là bội chung của 3 và 5)
- Số này là bội của 15, từ 1-100 có số
- Vậy số đèn tắt thêm = 20 - 6 = 14 lồng đèn
Tổng số lồng đèn đã tắt = 33 + 14 = 47 lồng đèn Số lồng đèn còn sáng = 100 - 47 = 53 lồng đèn
Đáp án:
a) 33
b) 53
Bài 2. (3 điểm)
Mùa giải Bundesliga (giải vô địch bóng đá Đức) năm 2024, đội Bayer Leverkusen lên ngôi vô địch với thành tích không thua trận nào sau 34 trận đấu, giành được 90 điểm.
Hỏi trong 34 trận trên, đội này có bao nhiêu trận thắng? Biết rằng mỗi trận thắng được 3 điểm, hòa được 1 điểm và thua thì không có điểm.
Điền kết quả vào chỗ trống: _________
Hướng dẫn chi tiết
Bài 2
Gọi x là số trận thắng, y là số trận hòa.
- Tổng số trận: x + y = 34 (do không có trận thua)
- Tổng số điểm: 3x + y = 90
Từ phương trình thứ nhất: y = 34 - x Thay vào phương trình thứ hai: 3x + (34 - x) = 90 ⟹ 3x + 34 - x = 90 ⟹ 2x = 90 - 34 = 56 ⟹ x = 28
Vậy số trận thắng là 28 trận.
Đáp án: 28
Bài 3. (6 điểm)
Để chuẩn bị sân khấu cho buổi lễ tổng kết năm học, nhà trường cần sơn các mặt của bậc tam cấp gỗ.
Mỗi bậc tam cấp đều có chiều rộng 3 dm, chiều dài 12 dm và chiều cao 2 dm (xem hình vẽ).
Tính tổng diện tích các mặt cần sơn của bậc tam cấp trên. Biết rằng không sơn mặt đáy và mặt sau của bậc tam cấp.
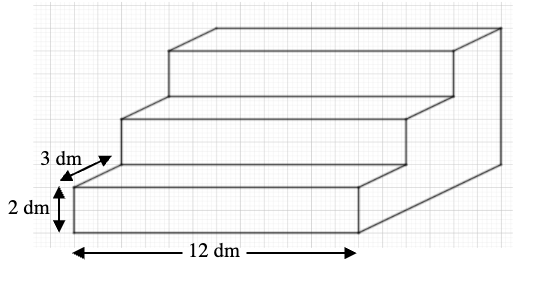
Yêu cầu:
Trình bày đầy đủ các bước giải bài toán vào phía dưới.
Hướng dẫn chi tiết
Bài 3
Lời giải theo đáp án tham khảo (252 dm²)
1. Phân tích các kích thước và các mặt cần sơn:
- Mỗi bậc tam cấp có: chiều dài 12 dm, chiều rộng (độ sâu của một mặt bậc) 3 dm, chiều cao 2 dm.
- Bậc tam cấp gồm 3 bậc.
- Không sơn mặt đáy (mặt dưới cùng của bậc thấp nhất) và mặt sau (mặt thẳng đứng lớn ở phía sau cùng của toàn bộ tam cấp).
2. Tính "Tổng diện tích các mặt trước" (theo cách gọi và tính trong đáp án tham khảo): Cách tính này gộp chung diện tích của các mặt trên (bề mặt bậc thang) và các mặt đứng phía trước (mặt vế thang).
- Diện tích 3 mặt trên (bề mặt các bậc):
- Mỗi mặt trên:
12 dm × 3 dm = 36 dm². - Ba mặt trên:
3 × 36 dm² = 108 dm².
- Mỗi mặt trên:
- Diện tích 3 mặt đứng phía trước (vế của các bậc):
- Mỗi mặt đứng:
12 dm × 2 dm = 24 dm². - Ba mặt đứng:
3 × 24 dm² = 72 dm².
- Mỗi mặt đứng:
- "Tổng diện tích các mặt trước" (theo đáp án tham khảo):
108 dm² + 72 dm² = 180 dm². (Hoặc theo công thức trong đáp án tham khảo:2 × 12 × 3 + 3 × 12 × 3 = 72 dm² + 108 dm² = 180 dm²).
3. Tính "Tổng diện tích các mặt bên" (theo cách tính trong đáp án tham khảo): Cách tính diện tích cho một mặt bên theo đáp án tham khảo là tổng của ba hình chữ nhật có chiều cao 2 dm và chiều dài (sâu) lần lượt là 9 dm, 6 dm, và 3 dm:
- Phần 1:
2 dm (cao) × 9 dm (sâu 3 bậc) = 18 dm². - Phần 2:
2 dm (cao) × 6 dm (sâu 2 bậc) = 12 dm². - Phần 3:
2 dm (cao) × 3 dm (sâu 1 bậc) = 6 dm². - Diện tích một mặt bên:
18 dm² + 12 dm² + 6 dm² = 36 dm². - "Tổng diện tích hai mặt bên" (theo đáp án tham khảo):
2 × 36 dm² = 72 dm². (Hoặc theo công thức trong đáp án tham khảo:(2 × 9 + 2 × 6 + 2 × 3) × 2 = (18 + 12 + 6) × 2 = 36 × 2 = 72 dm²).
4. Tổng diện tích các mặt cần sơn:
Cộng kết quả từ mục 2 và mục 3:
180 dm² + 72 dm² = 252 dm².
Đáp án (theo đáp án tham khảo): 252 dm²
Lưu ý
- Thí sinh ghi đáp số vào phần "Điền kết quả" ở bài 1 và bài 2.
- Thí sinh trình bày đầy đủ các bước giải của Bài 3.
- Không viết vào phần gạch chéo trên giấy thi.
HẾT